MCAI Economics Vision: MindCast AI Field-Geometry Reasoning
A Unifying Framework for Structural Explanation in Law, Economics and Artificial Intelligence
Executive Summary
Modern debates in economics, law, technology policy, and artificial intelligence often misdiagnose failure by attributing outcomes to intent, ethics, or competence—even when the same outcomes recur across different actors and institutions. Persistent convergence signals a different explanatory regime: structural constraints dominate behavior once systems reach scale.
Albert Einstein supplied the template for this shift in reasoning. General relativity explains gravity not as motive or force, but as geometry: mass curves spacetime, and motion follows survivable paths shaped by that curvature. Asking why objects move is less informative than identifying the geometry that makes alternative motion unsustainable.
Chicago Law and Economics adopted this same logic in institutional form. Landes and Posner’s gravity analogies in Economic Analysis of Law describe efficiency as an attractor produced by structural instability, not judicial intent. Behavioral economics completes the picture by showing that cognitive frictions curve choice from within, just as transaction costs curve institutions from without.
This publication introduces MindCast AI Field-Geometry Reasoning (FGR), a primary interpretive framework that formalizes the shared Einstein-Landes-Posner logic. FGR determines when outcomes are governed by constraint geometry rather than intent, and when foresight simulation is necessary versus when structural explanation alone is sufficient. A single national case—the National Quantum Initiative—demonstrates how high intent and investment can coexist with predictable drift when no downhill path connects discovery, deployment, and governance.
I. The Explanatory Error in Modern Policy and Strategy
Modern policy, legal, and strategic analysis routinely misattributes systemic outcomes to intent, ethics, or competence. Repeated convergence across actors with divergent values signals a deeper mechanism at work. Mechanical repetition indicates that structural constraints dominate behavior once systems reach scale. Identifying this error is essential before any predictive or reform‑oriented analysis can begin.
Intent‑based explanations and repeated failure
Moral narratives versus mechanical outcomes
The signal of structural dominance
II. Einstein’s Method: From Force to Geometry
Albert Einstein’s contribution was methodological before it was physical. General relativity replaced force‑based explanation with geometric description, showing that motion follows from environmental structure rather than causal intent. Curvature determines which paths are survivable and which collapse. This shift provides a transferable logic for analyzing any complex system governed by constraints.
Gravity as structure, not cause
Curvature, geodesics, and survivable motion
Why motive‑seeking explanations mislead in complex systems
III. Chicago Law and Behavioral Economics as Institutional Geometry
Chicago Law and Economics and behavioral economics describe complementary layers of a single structural system rather than competing theories. The traditional Chicago School explains how external rules, prices, and transaction costs curve institutional space. Behavioral economics explains how cognitive frictions curve choice from the inside. Together, they form a unified geometry in which external constraints and internal limits jointly determine survivable paths.
A. External Institutional Geometry (Chicago Law and Economics)
Chicago Law and Economics adopted structural reasoning long before it was named explicitly. Coase, Becker, Posner, and Landes analyzed law as a system shaped by transaction costs, incentive gradients, and instability pressures. Legal outcomes converged because some configurations persisted under pressure while others failed. Institutional regularities emerged without reliance on judicial psychology or moral narrative.
Coase: transaction costs as curvature
Becker: incentive gradients and drift
Posner and Landes: efficiency as a structural attractor
B. Internal Cognitive Geometry (Behavioral Economics)
Behavioral economics extends the same constraint‑based reasoning inside the decision‑maker. Cognitive load, salience, loss aversion, and bounded attention operate as internal frictions that shape feasible choice. These forces do not merely bias rational calculation; they reshape the internal decision landscape itself. Behavioral regularities persist because cognition exhibits geometry just as institutions do.
Cognitive frictions as internal transaction costs
Salience, bias, and bounded attention
Why behavior repeats even under awareness
Contact mcai@mindcast-ai.com to partner with us on economics and innovation foresight simulation. Recent works: White House Genesis Mission x NIBE (Nov 2025), The Economic Architecture Behind Malcolm Gladwell’s Worldview (Dec 2025), Foresight on Trial, The Diageo Litigation (Jan 2026).
IV. MindCast AI Field‑Geometry Reasoning (FGR)
MindCast AI Field‑Geometry Reasoning formalizes the shared logic of Einsteinian physics and Chicago Law and Behavioral Economics into a single operational framework. The method models outcomes as the result of interacting external and internal constraint fields. Stability replaces intention as the primary explanatory variable. Prediction follows from identifying which paths can endure. Field‑Geometry Reasoning functions as a primary interpretive Vision within MindCast AI, determining when foresight simulation is necessary and when structural explanation alone is sufficient.
Core Parameters and Metrics
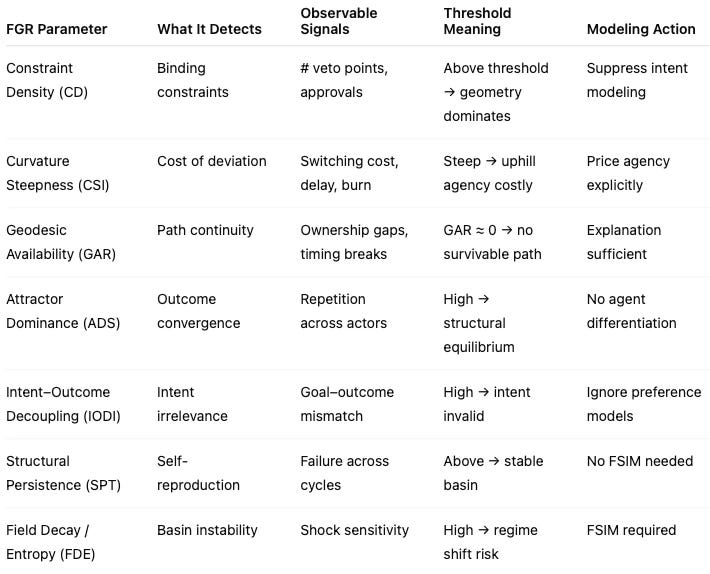
Field‑Geometry Reasoning relies on diagnostic parameters rather than outcome scores. These measures determine whether behavior is geometry‑dominated, whether intent‑based modeling is valid, and whether foresight simulation adds signal or noise. To avoid rhetorical use, each parameter is calibrated against historical classes of cases and evaluated relative to threshold bands rather than absolute values.
Constraint Density (CD) – Measures how many independent constraints simultaneously bind action, including veto points, regulatory overlap, coordination actors, and sequential approvals. Geometry dominance typically emerges once CD exceeds a system‑specific threshold where no single actor can relax constraints unilaterally. Calibration occurs by comparison to known coordination failures and successful low‑CD regimes.
Curvature Steepness Index (CSI) (geometry‑specific) – Measures the cost of deviating from dominant paths, including switching costs, time delays, exit penalties, and capital burn. Steep curvature exists when deviation costs exceed feasible actor tolerance within the system’s operating horizon. CSI is evaluated comparatively across adjacent paths rather than in isolation.
Geodesic Availability Ratio (GAR) – Assesses whether a continuous, survivable path exists from intent through execution to outcome. GAR approaches zero when authority, incentives, or timing break continuity between stages. Positive GAR indicates that reform or coordination can plausibly alter motion without wholesale field redesign.
Attractor Dominance Score (ADS) – Measures the strength of outcome convergence across different actors, leadership regimes, and time periods. High ADS indicates that outcomes repeat despite variation in intent, signaling structural equilibrium. ADS is validated through cross‑case recurrence rather than single‑instance failure.
Intent–Outcome Decoupling Index (IODI) – Measures the degree to which stated goals, reforms, or leadership changes fail to influence outcomes. High IODI suppresses motive‑based modeling and indicates that internal preferences are overridden by external geometry.
Structural Persistence Threshold (SPT) – Determines whether failure modes self‑correct or self‑reproduce despite reform. Systems above SPT exhibit persistence across cycles of intervention, indicating that explanation alone is sufficient absent geometry change.
Field Decay / Constraint Entropy (FDE) – Measures the rate at which constraint fields weaken, tighten, or reconfigure over time due to exogenous shocks such as technological breakthroughs, financial crises, legal rulings, or geopolitical events. Rising entropy indicates basin instability or evaporation, while low entropy signals durable curvature. FDE calibrates how quickly attractors may dissolve or invert, converting static geometry into a time‑dependent field.
Together, these parameters gate downstream modeling by identifying geometry‑dominant regimes, distinguishing conditional curvature from inevitability, and determining whether foresight simulation is warranted. Field Decay further specifies when geometry itself is transient, signaling when foresight simulation is required to model regime transitions rather than steady drift.
Internal–External Geometry Interaction
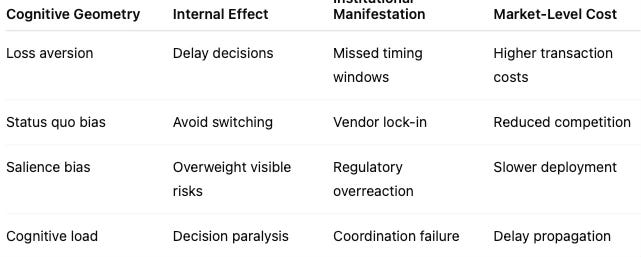
Field‑Geometry Reasoning does not deny agency; it prices it. Internal cognitive geometry determines how much effort an actor must expend to resist or redirect external institutional curvature. Behavioral frictions such as loss aversion, salience bias, and status‑quo anchoring raise the internal cost of pursuing uphill paths, while institutional geometry determines whether those costs compound or dissipate over time.
Cognitive geometry manifests institutionally when internal hesitation translates into delayed action, risk aversion, or coordination failure. A loss‑averse executive facing steep institutional curvature defers investment, which appears externally as higher transaction costs, slower bargaining, or missed timing windows. Internal geometry therefore becomes external friction through aggregation, converting psychology into market‑level drag.
This interaction allows FGR to model the cost of agency. Actors can move uphill, but the Curvature Steepness Index specifies how much capital, political will, or reputational risk must be burned to do so. Agency exists, but it is constrained, priced, and often exhausted before geometry changes.
Simulation Routing and Threshold Testing
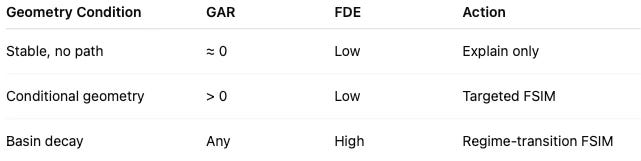
Field‑Geometry Reasoning treats geometry as time‑dependent rather than static. When Field Decay is high, stable basins may evaporate, invert, or fragment, making static explanation insufficient even when current geometry dominates. In such regimes, foresight simulation becomes necessary to model phase transitions, shock absorption, and post‑shock re‑equilibration.
Field-Geometry Reasoning routes analysis toward foresight simulation only after leverage has been identified. At this stage, simulation is used to test timing, thresholds, and sequencing rather than to rediscover structure. Simulation becomes appropriate when geometry is conditional, when perturbations plausibly reshape slope, or when multiple intervention paths compete.
Routing decisions depend on whether marginal changes alter Geodesic Availability Ratio or merely redistribute motion within an existing attractor. When geometry dominates and geodesics are absent, Field-Geometry Reasoning explains outcomes without simulation. When geometry is malleable and thresholds are unstable, foresight simulation becomes the correct tool for sequencing intervention.
Formal definition
Field, Geometry, Motion framework
Stability versus optimality
Prediction by identifying what cannot persist
V. Visual Model: Field → Geometry → Motion
The Field–Geometry–Motion model renders structural reasoning intuitively visible. Constraint fields shape the topology of choice by creating gradients, basins, and cliffs. Geometry channels behavior toward survivable equilibria without requiring deliberation. Motion describes the resulting drift over time.
External constraint field
Choice geometry and basins of attraction
Geodesic behavioral drift
VI. Application: National-Scale Innovation Under Structural Constraint
National-scale innovation offers the cleanest empirical setting for Field-Geometry Reasoning because intent, funding, and political consensus are unusually explicit, yet outcomes still converge toward delay and fragmentation. When large public investments repeatedly fail to translate into deployment, the failure cannot be explained by ambition, intelligence, or scientific uncertainty. Structural timing, coordination density, and institutional alignment dominate outcomes once innovation crosses from research into execution. At this scale, innovation succeeds or fails based on whether the field contains a downhill path.
MindCast AI’s National Innovation Behavioral Economics (NIBE) framework treats innovation as a throughput problem rather than a discovery problem. Progress depends on synchronization across institutions, control of delay propagation, and narrative coherence across agencies and markets. The core metrics—Temporal Drag Coefficient (TDC), Synchronization Integrity Score (SIS), Delay Propagation Index (DPI), Narrative Latency Gap (NLG), and Throughput Coherence Quotient (TCQ)—provide a way to measure whether innovation geometry accelerates motion or traps it.
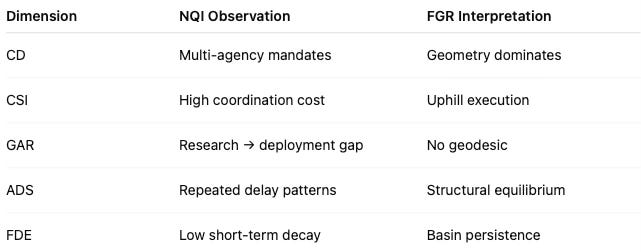
The National Quantum Initiative: A Canonical Case of Structural Drag
The National Quantum Initiative Reauthorization Act illustrates gravity without a geodesic. Congressional authorization, agency mandates, and funding streams are distributed across institutions operating on different clocks and incentive structures. Research capacity and publication output increase, yet commercialization, procurement, and deployment remain structurally uphill. No actor occupies a continuous, survivable path from discovery to application.
From a Field-Geometry perspective, the problem is not insufficient oversight or inadequate funding. The problem is curvature. Fragmented authority increases temporal drag, weakens synchronization integrity, and amplifies delay propagation across the innovation stack. Reauthorization marginally improves local efficiency but leaves the global geometry unchanged, producing persistence rather than correction.
The National Quantum Initiative therefore functions as a reference case for national innovation under structural constraint. High intent and high investment coexist with predictable drift because the field lacks a downhill path that connects research, deployment, and governance. The foresight question is not whether quantum technology will advance, but whether the institutional geometry will ever allow advancement to become inertial rather than aspirational.
VII. When Foresight Simulation Is Warranted
Field‑Geometry Reasoning clarifies when foresight simulation adds value and when it does not. Simulation becomes useful only after structural dominance has been established and when timing, thresholds, or intervention sequencing remain indeterminate. In geometry‑dominated systems with no viable geodesics, explanation alone is sufficient; simulation would merely restate inevitability.
When curvature is conditional or when modest field redesign could plausibly open a downhill path, foresight simulation operationalizes insight into action. Simulation maps curvature variables, tests perturbations, and identifies irreversibility thresholds where small changes produce large downstream effects. Used correctly, simulation converts structural diagnosis into decision leverage rather than narrative prediction.
Mapping curvature variables
Perturbation scenarios
Irreversibility thresholds and timing windows
VIII. Strategic and Policy Implications
Field‑Geometry Reasoning reframes strategy and policy away from exhortation and toward field design. Many reforms fail because they attempt to push behavior uphill instead of altering the constraints that define survivable paths. Effective intervention reshapes coordination density, timing alignment, and incentive curvature so that desired outcomes become inertial rather than aspirational.
For policymakers, this implies prioritizing institutional synchronization over isolated oversight and focusing on geometry‑changing interventions rather than input expansion. For firms and regulators, the framework clarifies which failures are structural and which remain contingent, guiding where effort can still matter.
What actors can change versus what geometry resists
Institutional synchronization and timing alignment
Redesigning fields instead of managing behavior
X. Conclusion: From Explanation to Foresight
Field‑Geometry Reasoning offers a general theory of institutional motion. Treating law, markets, technology, and cognition as geometric systems explains convergence and failure without moral confusion. Foresight replaces post hoc narrative with structural anticipation. Designing better futures requires redesigning the fields in which decisions unfold.
Why geometry outperforms narrative
Institutional design as curvature management
Field‑Geometry Reasoning as a general theory of institutional motion